What Is Radioactivity? What is Radiation?

Definition of Radioactivity and Radiation: Unstable atomic nuclei will spontaneously decompose to form nuclei with a higher stability. The decomposition process is called radioactivity. The energy and particles which are released during the decomposition process are called radiation. When unstable nuclei decompose in nature, the process is referred to as natural radioactivity. When the unstable nuclei are prepared in the laboratory, the decomposition is called induced radioactivity.

Answer: There are three major types of natural radioactivity:

1. Alpha Radiation

Alpha radiation consists of a stream of positively charged particles, called alpha particles, which have an atomic mass of 4 and a charge of +2 (a helium nucleus). When an alpha particle is ejected from a nucleus, the mass number of the nucleus decreases by four units and the atomic number decreases by two units. For example:

²³⁸₉₂U -> ⁴₂He + ²³⁴₉₀Th

The helium nucleus is the alpha particle.

2. Beta Radiation

Beta radiation is a stream of electrons, called beta particles. When a beta particle is ejected, a neutron in the nucleus is converted to a proton, so the mass number of the nucleus is unchanged, but the atomic number increases by one unit. For example:

²³⁴₉₀ -> ⁰_-1e + ²³⁴₉₁Pa

The electron is the beta particle.

3. Gamma Radiation

Gamma rays are high-energy photons with a very short wavelength (0.0005 to 0.1 nm). The emission of gamma radiation results from an energy change within the atomic nucleus. Gamma emission changes neither the atomic number nor the atomic mass. Alpha and beta emission are often accompanied by gamma emission, as an excited nucleus drops to a lower and more stable energy state.

Alpha, beta, and gamma radiation also accompany induced radioactivity. Radioactive isotopes are prepared in the lab using bombardment reactions to convert a stable nucleus into one which is radioactive. Positron (particle with the same mass as an electron, but a charge of +1 instead of -1) emission isn't observed in natural radioactivity, but it is a common mode of decay in induced radioactivity. Bombardment reactions can be used to produce very heavy elements, including many which don't occur in nature.

Introduction to Molecular Geometry

Introduction to Molecular Geometry: Molecular Geometry or molecular structure is the three-dimensional arrangement of atoms within a molecule. It is important to be able to predict and understand the molecular structure of a molecule because many of the properties of a substance are determined by its geometry.

Molecular geometry angles contain a range of question, as we have large number of results about geometry angles. Molecular geometry angles exist as person as well as with lot of other geometric figures. Most of the molecular geometry angles figures are specified by their angles, like square, rectangles, triangles etc. since of so wide presence geometric angle have lot of results in them. These lots of results make a wide range of molecular geometry angles.

The Valence Shell, Bonding Pairs, and VSEPR Model

The outermost electrons of an atom are its valence electrons. The valence electrons are the electrons that are most often involved in forming bonds and making molecules.

Pairs of electrons are shared between atoms in a molecule and hold the atoms together. These pairs are called "bonding pairs".

One way to predict the way electrons within atoms will repel each other is to apply the VSEPR (valence-shell electron-pair repulsion) model. VSEPR can be used to determine a molecule's general geometry.

Predicting Molecular Geometry

Here is a chart that describes the usual geometry for molecules based on their bonding behavior. To use this key, first draw out the Lewis structure for a molecule. Count how many electron pairs are present, including both bonding pairs and lone pairs. Treat both double and triple bonds as if they were single electron pairs. A is used to represent the central atom. B indicates atoms surrounding A. E indicates the number of lone electron pairs. Bond angles are predicted in the following order:

lone pair versus lone pair repulsion > lone pair versus bonding pair repulsion > bonding pair versus bonding pair repulsion

Molecular Geometry

Internal vs. External Forces

Internal vs. External Forces

There are a variety of ways to categorize all the types of forces. All the types of forces can be categorized as contact forces or as action-at-a-distance forces. Whether a force was categorized as an action-at-a-distance force was dependent upon whether or not that type of force could exist even when the objects were not physically touching. The force of gravity, electrical forces, and magnetic forces were examples of forces which could exist between two objects even when they are not physically touching. In this lesson, we will learn how to categorize forces based upon whether or not their presence is capable of changing an object's total mechanical energy. We will learn that there are certain types of forces, which when present and when involved in doing work on objects will change the total mechanical energy of the object. And there are other types of forces which can never change the total mechanical energy of an object, but rather can only transform the energy of an object from potential energy to kinetic energy (or vice versa). The two categories of forces are referred to as internal forces and external forces.

Forces can be categorized as internal forces or external forces. There are many sophisticated and worthy ways of explaining and distinguishing between internal and external forces. Many of these ways are commonly discussed at great length in physics textbooks. For our purposes, we will simply say that external forces include the applied force, normal force, tension force, friction force, and air resistance force. And for our purposes, the internal forces include the gravity forces, magnetic force, electrical force, and spring force.

Internal Forces	External Forces
Fgrav Fspring	Fapp Ffrict Fair Ftens Fnorm

The importance of categorizing a force as being either internal or external is related to the ability of that type of force to change an object's total mechanical energy when it does work upon an object. When net work is done upon an object by an external force, the total mechanical energy (KE+PE) that object is changed. If the work is positive work, then the object will gain energy. If the work is negative work, then the object will lose energy. The gain or loss in energy can be in the form of Potential Energy, kinetic energy, or both. Under such circumstances, the work which is done will be equal to the change in mechanical energy of the object. Because external forces are capable of changing the total mechanical energy of an object, they are sometimes referred to as nonconservative forces.

When the only type of force doing net work upon an object is an internal force (for example, gravitational and spring forces), the total mechanical energy (KE+PE) that object remains constant. In such cases, the object's energy changes form. For example, as an object is "forced" from a high elevation to a lower elevation by gravity, some of the potential energy of that object is transformed into kinetic energy. Yet, the sum of the kinetic and potential energies remain constant. When the only forces doing work are internal forces, energy changes forms - from kinetic to potential (or vice versa); yet the total amount of mechanical is conserved. Because internal forces are capable of changing the form of energy without changing the total amount of mechanical energy, they are sometimes referred to as conservative forces.

Electric Field Lines

Electric Field Lines

The magnitude or strength of an electric field in the space surrounding a source charge is related directly to the quantity of charge on the source charge and inversely to the distance from the source charge. The direction of the electric field is always directed in the direction that a positive test charge would be pushed or pulled if placed in the space surrounding the source charge. Since electric field is a vector quantity, it can be represented by a vector arrow. For any given location, the arrows point in the direction of the electric field and their length is proportional to the strength of the electric field at that location. Such vector arrows are shown in the diagram below. Note that the length of the arrows are longer when closer to the source charge and shorter when further from the source charge.

A more useful means of visually representing the vector nature of an electric field is through the use of electric field lines of force. Rather than draw countless vector arrows in the space surrounding a source charge, it is perhaps more useful to draw a pattern of several lines which extend between infinity and the source charge. These pattern of lines, sometimes referred to as electric field lines, point in the direction which a positive test charge would accelerate if placed upon the line. As such, the lines are directed away from positively charged source charges and toward negatively charged source charges. To communicate information about the direction of the field, each line must include an arrowhead which points in the appropriate direction. An electric field line pattern could include an infinite number of lines. Because drawing such large quantities of lines tends to decrease the readability of the patterns, the number of lines are usually limited. The presence of a few lines around a charge is typically sufficient to convey the nature of the electric field in the space surrounding the lines.

Charge Interactions Revisited

Charge Interactions are Forces

It is possible that we might have watched two balloons repel each other a dozen or more times and never even thought of the balloon interaction as being a force. Or perhaps you have used a plastic golf tube or other object to raise small paper bits off the lab table and never thought of Newton's laws of motion. Perhaps even now you're thinking "Why should I? That was the Newton's Laws unit and this is the Static Electricity unit." True. However, the physical world which we study does not separate itself into separate topics as we teachers and students are prone to do. Physics has an amazing way of fitting together in a seamless fashion. The information which you have forgotten about from the Newton's laws unit has a mischievous way of creeping up on you in other units. That forgetfulness (or negligence or mere ignorance) will haunt you as you try to learn new physics. The more physics which you learn (as in really learn), the more that you come to recognize that the pieces of the physics puzzle fit together to form a unified picture of the world of sight, sound, touch and feel. Here we will explore how Newton's laws of motion fit together with the interaction of charged objects.

Suppose that you hold a charged plastic golf tube above a handful of paper bits at rest on the table. The presence of the charged tube is likely to polarize a few bits of paper and then begin to exert an upward pull upon them. The attraction between a charged tube and a polarized (yet neutral) paper bit is an electrical force - F_elect. Like all the

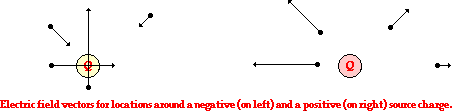
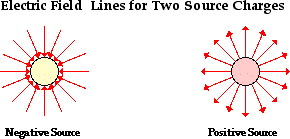
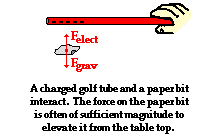forces studied in The Physics Classroom, the electrical force is a push or pull exerted upon an object as a result of an interaction with another object. The interaction is the result of electrical charges and thus it is called an electrical force.

Unlike many forces which we study, the electrical force is a non-contact force - it exists despite the fact that the interacting objects are not in physical contact with each other. The two objects can act over a separation distance and exert an influence upon each other. In this case, the plastic golf tube pulls upward upon the paper bit and a paper bit pulls downward upon the golf tube. In this case, the force is significantly small. If you were holding the golf tube, you would not likely sense the downward pull exerted upon it by the paper bit. On the other hand, the force is often large enough to either balance or even overwhelm the downward pull of gravity (F_grav) upon the paper bit and cause it to be elevated or even accelerated off the table. Of course the actual result of the force upon the paper bit is related to Newton's laws and a free-body analysis. If at any moment, the electrical force is greater in magnitude than the gravitational force, the paper bit would be accelerated upward. And if at any moment, the electrical force is equal in magnitude to the gravitational force, the paper bit will be suspended (or levitated) in midair. The paper bit would be said to be at equilibrium.

Now consider the case of the rubber balloons hanging by light threads from the ceiling. If each balloon is rubbed in the same manner (with animal fur), they each become negatively charged and exert a repulsive affect upon each other. This charge interaction results in a force upon each balloon which is directed away from the balloon with which it interacts. Once more, we can identify this repulsive affect as an electrical force. This electrical force joins two other forces which act upon the balloon - the tension force and a force of gravity. Since the balloons are at rest, the three forces must balance each other such that the net force is zero.

Both of these examples illustrate how the interaction between two charges results in a mutual force acting upon the charged objects. An electrical interaction is a force which, like any force, can be analyzed using a free-body diagram and Newton's laws. But what factors affect the magnitude of this force? Is there an equation which can be used to quantify it the same manner as was done for the force of gravity (F_grav = m•g) and the force of friction (F_frict = mu•F_norm)? The answer is Yes! Coulomb's law holds the key to understanding the answer to these questions.

How Can an Insulator be Polarized?

How Can an Insulator be Polarized?

Polarization can occur within insulators, but the process occurs in a different manner than it does within a conductor. In a conducting object, electrons are induced into movement across the surface of the conductor from one side of the object to the opposite side. In an insulator, electrons merely redistribute themselves within the atom or molecules nearest the outer surface of the object. To understand the electron redistribution process, it is important to take another brief excursion into the world of atoms, molecules and chemical bonds.

The electrons surrounding the nucleus of an atom are believed to be located in regions of space with specific shapes and sizes. The actual size and shape of these regions is determined by the high-powered mathematical equations common to Quantum Mechanics. Rather than being located a specific distance from the nucleus in a fixed orbit, the electrons are simply thought of as being located in regions often referred to as electron clouds. At any given moment, the electron is likely to be found at some location within the cloud. The electron clouds have varying density; the density of the cloud is considered to be greatest in the portion of the cloud where the electron has the greatest probability of being found at any given moment. And conversely, the electron cloud density is least in the regions where the electron is least likely to be found. In addition to having varying density, these electron clouds are also highly distortable. The presence of neighboring atoms with high electron affinity can distort the electron clouds around atoms. Rather than being located symmetrically about the positive nucleus, the cloud becomes asymmetrically shaped. As such, there is a polarization of the atom as the centers of positive and negative charge are no longer located in the same location. The atom is still a neutral atom; it has just become polarized.

The discussion becomes even more complex (and perhaps too complex for our purposes) when we consider molecules - combination of atoms bonded together. In molecules, atoms are bonded together as protons in one atom attract the electrons in the clouds of another atom. This electrostatic attraction results in a bond between the two atoms. Electrons are shared by the two atoms as they begin to overlap their electron clouds. If the atoms are of different types (for instance, one atom is Hydrogen and the other atom is Oxygen), then the electrons within the clouds of the two atoms are not equally shared by the atoms. The clouds become distorted, with the electrons having the greatest probability of being found closest to the more electron-greedy atom. The bond is said to be a polar bond. The distribution of electrons within the cloud is shifted more towards one atom than towards the other atom. This is the case for the two hydrogen-oxygen bonds in the water molecule. Electrons shared by these two atoms are drawn more towards the oxygen atom than towards the hydrogen atom. Subsequently, there is a separation of charge, with oxygen having a partially negative charge and hydrogen having a partially positive charge.

It is very common to observe this polarization within molecules. In molecules which have long chains of atoms bonded together, there are often several locations along the chain or near the ends of the chain that have polar bonds. This polarization leaves the molecule with areas which have a concentration of positive charges and other areas with a concentration of negative charges. This principle is utilized in the manufacture of certain commercial products which are used to reduce static cling. The centers of positive and negative charge within the product are drawn to excess charge residing on the clothes. There is a neutralization of the static charge buildup on the clothes, thus reducing their tendency to be attracted to each other. (Other products actually use a different principle. During manufacturing, a thin sheet is soaked in a solution containing positively charged ions. The sheet is tossed into the dryer with the clothes. Being saturated with positive charges, the sheet is capable of attracting excess electrons which are scuffed off of clothes during the drying cycle.)

Mathematics of Satellite Motion

Mathematics of Satellite Motion

The motion of objects are governed by Newton's laws. The same simple laws which govern the motion of objects on earth also extend to the heavens to govern the motion of planets, moons, and other satellites. The mathematics which describes a satellite's motion are the same mathematics presented for circular motion. In this part we will be concerned with the variety of mathematical equations which describe the motion of satellites.

Consider a satellite with mass M_sat orbiting a central body with a mass of mass M_Central. The central body could be a planet, the sun or some other large mass capable of causing sufficient acceleration on a less massive nearby object. If the satellite moves in circular motion, then the net centripetal force acting upon this orbiting satellite is given by the relationship

F_net = ( M_sat • v² ) / R

This net centripetal force is the result of the gravitational force which attracts the satellite towards the central body and can be represented as

F_grav = ( G • M_sat • M_Central ) / R²

Since F_grav = F_net, the above expressions for centripetal force and gravitational force can be set equal to each other. Thus,

(M_sat • v²) / R = (G • M_sat • M_Central ) / R²

Observe that the mass of the satellite is present on both sides of the equation; thus it can be canceled by dividing through by M_sat. Then both sides of the equation can be multiplied by R, leaving the following equation.

v² = (G • M_Central ) / R

Taking the square root of each side, leaves the following equation for the velocity of a satellite moving about a central body in circular motion

where G is 6.673 x 10^-11 N•m²/kg², M_central is the mass of the central body about which the satellite orbits, and R is the radius of orbit for the satellite.

Similar reasoning can be used to determine an equation for the acceleration of our satellite that is expressed in terms of masses and radius of orbit. The acceleration value of a satellite is equal to the acceleration of gravity of the satellite at whatever location which it is orbiting. In below, the equation for the acceleration of gravity was given as

g = (G • M_central)/R²

Thus, the acceleration of a satellite in circular motion about some central body is given by the following equation

where G is 6.673 x 10^-11 N•m²/kg², M_central is the mass of the central body about which the satellite orbits, and R is the average radius of orbit for the satellite.

The final equation which is useful in describing the motion of satellites is Newton's form of Kepler's third law. Since the logic behind the development of the equation has been presented elsewhere, only the equation will be presented here. The period of a satellite (T) and the mean distance from the central body (R) are related by the following equation:

where T is the period of the satellite, R is the average radius of orbit for the satellite (distance from center of central planet), and G is 6.673 x 10^-11 N•m²/kg².

There is an important concept evident in all three of these equations - the period, speed and the acceleration of an orbiting satellite are not dependent upon the mass of the satellite.

None of these three equations has the variable M_satellite in them. The period, speed and acceleration of a satellite is only dependent upon the radius of orbit and the mass of the central body which the satellite is orbiting. Just as in the case of the motion of projectiles on earth, the mass of the projectile has no affect upon the acceleration towards the earth and the speed at any instant. When air resistance is negligible and only gravity is present, the mass of the moving object becomes a non-factor. Such is the case of orbiting satellites.